Bond Valence Sum

Introduction to Bond Valence Method

The Bond Valence Model (Brese & O’Keeffe, 1991; Brown, 2009) is an important approach to assessing the chemical plausibility of inorganic crystal structure. The model is based on the valence sum rule from the Pauling’s electrostatic valence concept (Pauling, 1929): the sum of bond valences $S_{ij}$ around any ion, $i$ , is equal to its valence, $V_i$ (the formal oxidation state)

$V_{i} = \sum\limits_{j} S_{ij}$ (1)

where the sum goes over all neighboring atoms $j$ of the atom $i$ .

The bond valence $S_{ij}$ can be considered a measure of the electrostatic flux between a cation and an anion, directly related with the strength of the bond and correlated inversely with bond length. It can be approximated by

$S_{ij} = exp (\frac{R_0 - R_{ij}}{B})$ (2)

where $R_0$ and $B$ are constant parameters and $R_{ij}$ is the interatomic distance between atoms $i$ and $j$ . For many bonds $B$ is close to 0.37. The bond valence parameters ( $R_0$ and $B$ ) used by the program were taken from a list compiled by I. D. Brown from various references and stored in a CIF file, bvparm2016.cif, available for download from https://www.iucr.org/resources/data/datasets/bond-valence-parameters. It should be noted, that bond valence parameters are not available for all pairs of atoms.

The most common application of the bond valence model is for checking and validating new crystal structures by comparing oxidation states (formal ionic charges) $V_i^0$ with bond valence sums $V_i$ calculated from the equations (1) and (2). The agreement is generally good if the structure is correct, but when the agreement is poor and large deviations are observed the structure determination might be wrong (e.g., incorrect symmetry or missing atoms) or inappropriate bond valence parameters were used.

Bond valence model is often used to explain the structural distortions from the ideal three-dimensional structure. These distortions are usually measured by using the global instability index, $G_{ii}$ , which is the root-mean-square value over the deviations $V_i - V_i^0$ of the atomic valence of all atoms from the bond valence sum:

$G_{ii} =\sqrt{ \frac{1}{N}\sum_{i=1}^{N}(V_i - V_i^0)^2}$

The $G_{ii}$ index is usually less than 0.1 v.u. in stable and well determined structures. Values between 0.1 and 0,2 v.u. can be associated to strained structures. Typically, room-temperature structures with $G_{ii}$ values greater than 0,2 v.u. are rare.

Bond valence sums are incorporated as restraints in the structure solution by real space methods.

Check the bond valence sums

To check the bond valence sums (BVS) of your crystal structure choose Bond Valence Sum in the Tools menu.
In the case of the phosphate AgTbP₂O₇ the test produce the following result.

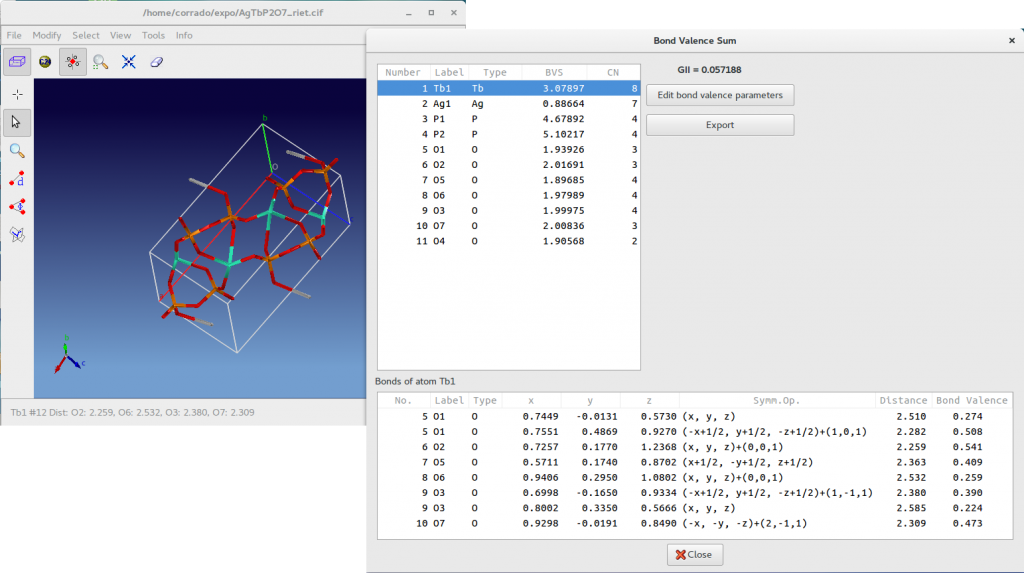
For each atom the BVS as well as the coordination numbers (CN) are reported in the above list box. The below list box contains the bond lengths and bond valences of all bonds that contribute to BVS of the selected atom. For example, in the above picture for the selected atom Tb1 you can see all the bond Tb-O contributing to the bond valence sum 3.08. In addition, fractional coordinates and the symmetry operator applied to the atom in the asymmetric unit are reported. The $G_{ii}$ is displayed and all the information accessible by this window can be exported in a text file pressing the button Export. The button Edit bond valence parameters enables the access to the bond valence parameters ( $R_0$ and $B$ ) corresponding to each pair of atom types.

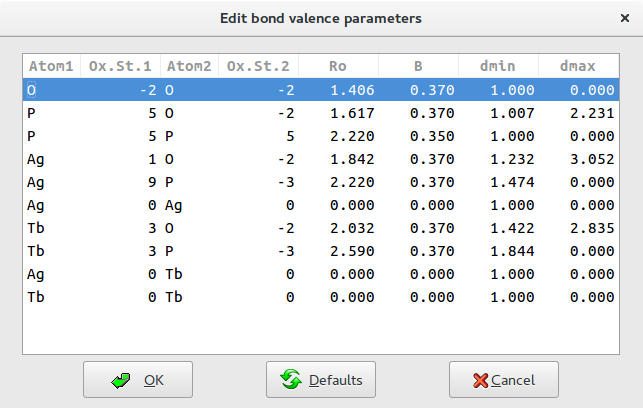
You will ensure the all information specified in this window are reasonable and if necessary modify the entries that are not valid.
For each pair the program search in the database the corresponding bond valence parameters and assign a bond windows, i.e. the range of distances between any two atoms that are to be considered as bonds. These range is defined in terms of $d_{min}$ and $d_{max}$ following some of the rules described by Altermatt and Brown (Altermatt & Brown, 1985).
It is assumed that the bonding occurs only between atoms of different electronegativity. This is the reason why bonds like P-P or O-O are excluded assigning value of $d_{min}=1$ and $d_{max}=0$ .
If the bond valence parameters corresponding to a pair is not available in the database, the parameters are set to $R_0=0$ , $B=0$ , $d_{min}=1$ and $d_{max}=0$ generating a contribution equal 0 to the BVS.
When the oxidation state is non specified by the user the program try to assign the most probable.

References

Altermatt, D & Brown, I.D. (1985). Acta Cryst. B41, 240-244.
Brese, N. E. & O’Keeffe, M. (1991). Acta Cryst. B47, 192–197.
Brown, I. D. (2009). Chem. Rev. 109, 6858–6919.
Pauling, L. (1929). J. Am. Chem. Soc., 51,1010.