As previously established, Sir2019 allows ab initio and non ab initio phasing, followed by phase extension and refinement. Tools for such purposes are the most popular phasing techniques like:
-
- Direct Methods, VLD, Patterson techniques for ab initio phasing;
-
- MR, SAD/MAD, techniques for non ab initio phasing;
- Phase extension and refinement methods.
The last category is coupled to all the remaining categories and will be described first.
EDM techniques
Their basic procedure may be described in three steps:
-
-
- Phases and weights, coupled with observed amplitudes, are used to calculate an electron density map.
- The Fourier inversion of the modified map should lead to new and more accurate target phase estimates and to their corresponding weights.
For high resolution data, Sir2019 adopted the FFTW routines by Frigo & Johnson (2005) coupled with a simple low density modification algorithm (Giacovazzo & Siliqi, 1997) similar to that suggested by Shiono & Woolfson (1992). Only a very small percentage (from 2.5% to 10%) of the pixels, those with the largest density values, are used for the Fourier inversion of the electron density map, the rest is set to zero (LDT modification). For lower resolution data, Sir2019 prefers to use the DM routine by Cowtan (1998) , except when the FL (Free Lunch, see below) techniques are used. - The LDT technique above described is applied to small molecules for extending and refining phases obtained by Direct Methods or by Patterson Techniques. More complete models are so obtained which may then be submitted to least squares.
For proteins , owing to the larger size of the molecules and to the limited data resolution, the above technique is not sufficient, and a more complex strategy, including a modified EDM procedure, is necessary.
Indeed, during density modification cycles, the molecular envelope of the protein (Wang, 1985; Leslie, 1987) is used as a mask in order to improve EDM efficiency (Burla, Carrozzini et al., 2003a). The protein volume is estimated through the Matthews (1968) formula and the envelope is calculated, for each trial solution, from the current phases. The electron density map is modified by assigning different weights to pixels falling inside or outside the envelope, so tentatively depleting the intensities of the false peaks. The map is then inverted and the resulting phases may improve their values.
-
RELAX procedure
The problem of well oriented but misplaced molecular fragments may be solved by the RELAX procedure (Burla, Carrozzini et al., 2002a; Caliandro et al., 2007). Data and corresponding phases of a trial solution obtained in the correct space group are extended and refined in P1 and a reduced number of EDM cycles are performed with no space-group symmetry imposed. Some figures of merit enable the determination of the shift to apply in the correct space group in order to re-establish the original space group symmetry.
The RELAX procedure is automatically applied in default ab initio runs of Sir2019.
Free lunch (FL)
Any modified electron density map allows the extrapolation of non-observed structure factors, beyond and behind the experimental resolution limit (Caliandro et al., 2005 a,b). The method is applied for two different purposes:
i) for increasing the rate of success of the ab initio phasing procedures during the phasing process, via the active use of the extrapolated reflections (Patterson techniques only);
ii) for improving the best electron density achievable by current phasing techniques. The combined active use of observed and extrapolated structure factors may lead to improved electron density maps and therefore, after their modification and Fourier inversion, to better phase estimates.
FL is automatically applied when data resolution is worse than 1.25 Å.
Vive la difference (VLD)
This algorithm, coupled with EDM techniques, may be used for ab initio phasing as well as for phase extension and refinement: it is based only on properties of a new difference electron density and on the observed Fourier synthesis.
In ab initio phasing (crystal structure solution of small and medium size molecules, as well as of proteins with atomic resolution data) random phases are assigned to the target structure factors F, an observed Fourier synthesis is calculated and suitably modified (2.5% of the pixels, those with the largest density are selected, the rest is set to zero) to obtain a starting random model. The Fourier inversion of such modified map provides the model structure factors Fp. A new type of difference Fourier synthesis (Burla, Caliandro et al., 2010) is calculated, which, suitably modified and inverted, provides the best estimates of the structure factors of the difference electron density (say Fq).
By definition Fp + Fq is the current best approximation of F, by which a new observed electron density is calculated. Cycles of electron density modifications are applied in order to provide, at the end, a new electron density from which a model density is derived as before described.
The procedure is cyclic and stops when a figure of merit suggests that the correct solution has been found (Burla, Giacovazzo et al., 2010, 2011). More recently (Burla, Carrozzini et al., 2011) the efficiency of the algorithm has been improved, by integrating the RELAX procedure (see above), and applied to proteins at atomic resolution.
VLD may be applied, in combination with EDM techniques, for non ab initio phasing (Burla, Carrozzini et al. 2011, 2012; Carrozzini et al., 2013a; Caliandro et al., 2014) to perform phase refinement of initial models arising from ab initio Patterson techniques or from MR and SAD/MAD.
Synergy – Phantom Derivative (PhD)
This approach (Giacovazzo, 2015) is applied for non ab initio approaches. It involves the creation of a large number of structures (called ancils), having random atomic positions, the same unit cell and the same space group of the target structure. The founding PhD conjecture was the following: random structures like the ancils, even if completely uncorrelated with a given target structure, may usefully contribute to refine its phases. The conjecture has been experimentally proved by Burla, Carrozzini et al. (2015a) when PhD was applied to electron density maps provided by MR techniques, and theoretically justified by Burla, Cascarano et al. (2017).
A simple perspective for understanding the method is the following.
From n ancils n derivatives may be created according to
ρd(j) = ρ + ρa(j), j = 1, 2……., n
where ρ is the target density, ρa(j) is the jth ancil density, and ρd(j) is the electron density of the jth derivative (it is called phantom since it is devoid of chemical meaning).
If a model density map ρp is available, the ρd(j)’s may be approximated by n derivative density estimates ρp + ρa(j), j = 1, 2……., n , which, submitted to EDM techniques, may provide more sound derivative densities ρdest(j) . Then the simple sum function
![]()
may provide a better estimate of ρ because the sum of the ρest(j) will emphasize the target features and the sum of the ρa(j) will contribute to the background.
Later on (Carrozzini et al., 2016) the concept of ancil was further on extended: an ancil may also be the same target structure shifted by a permissible translation. The advantage of this choice is that amplitudes and phases of the derivative (target + shifted target) are related via simple trigonometric relations to amplitudes and phases of the target structure:
|Fdh| = 2|Fh||cos(πht)|, φdh = φh + πht.
The use of such new type of ancil is fully competitive with the results obtained when the ancils are randomly fixed and is much faster: therefore it is the default choice of Sir2019.
Phase driven refinement of a molecular model (PDRF)
Current crystallographic least squares minimize the quantity
![]()
If some previous information on φh is available, then the more general expression
![]()
which minimizes the |Fqh| amplitudes, and is referred in literature (Arnold & Rossmann, 1988) as vector refinement. Its doubles the number of observational equations, because it minimizes functions of amplitudes and of phases. Vector refinement has been implemented in REFMAC (Murshudov et al., 1997) via maximum likelihood techniques.
If the available molecular model structure is improved by EDM-VLD-FL-PhD techniques, then the application of PDRF would lead to a model automatically fitting the best available electron density, without passing through the model building step which, if the model is still inaccurate, is expected to fail. PDRF may be cyclically applied for improving the efficiency of the phase refinement after the MR step.
PDRF has been successfully introduced in the Sir2019 pipeline for MR (Carrozzini et al., 2015).
CAB: a cyclic automatic model-building procedure
BUCCANEER (Cowtan K., 2006) has been included in a cyclic procedure (CAB) aiming at increasing its rate of success and the quality of the provided molecular models without modifying its basic algorithms . The model phases provided by the first application of Buccaneer are modified in order to allow next Buccaneer applications more deeply exploiting the information provided by the phases originally used as input for CAB. The success of the experimental tests suggested to extend CAB to nucleic acids: the procedure allows the use of PHENIX.AUTOBUILD (Terwilliger et al, 2008) , NAUTILUS (Cowtan K., 1994) and ARP/wARP (Perrakis et al, 1999) , again without modifying their basic algorithms.
STOP to Phase Refinement procedure
For small/medium-sized structures the correctness of a solution is assessed, at the end of the DSR process, by the crystallographic residual factor (Rf) calculated via a diagonal least squares procedure: if the final value of Rf is smaller than a given threshold (default value 25%) the program stops; otherwise the program explores the next ranked phase set.
For large sized molecules and proteins the least squares are very time consuming: furthermore they cannot be applied to non-atomic resolution data without the use of supplementary information on the molecular geometry (here not considered). To recognize the correct solution a suitable figure of merit (fFOM) has been devised and applied at the end of the DSR process. The correct solution should be identified by large values of fFOM. Further details are quoted in Caliandro et al. (2014).
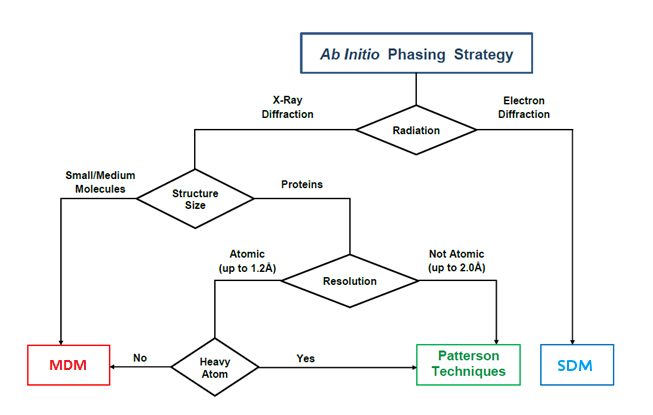
According to circumstances, the ab initio Sir2019 phasing process may apply Modern Direct Methods (MDM), Standard Direct Methods (SDM), VLD or Patterson procedures. To preserve its efficiency the program distinguishes different categories of structures: XSmall molecules (up to 5 atoms per asymmetric unit), Small (up to 80), Medium (up to 300), Large (up to 600), XLarge (up to 1000), XXLarge (up to 1750), Huge (no upper limit).
According to user preferences and to the presence or absence of heavy atoms, a different approach (Direct Methods, VLD or Patterson techniques) may be applied. The DSR procedure, mainly based on electron density modification (EDM) techniques, may be accomplished in different ways (it requires increasing computing times moving from XSmall to Huge structures). We shortly describe the various tools the user may employ in the phasing process.
The Sir2019 flow diagram, shown below, is a useful guide for understanding the program strategy for ab initio structure solution.
Modern Direct Methods (MDM) procedure
The approach is of multisolution type (Burla, Carrozzini et al., 2015b, 2017). It starts from random phases and applies a tangent like formula simultaneously using:
-
the P10 formula, based on the second representation of the triplet invariant. For each triplet the reciprocal space is explored, to provide a contribution which is summed to the Cochran contribution. Negative estimated triplets are then available;
-
the PSI-0 triplets, which in other programs are passively employed as a figure of merit for recognizing the correct solution;
-
negative quartet invariants via their first representation.
The phases obtained via the tangent step are then submitted to the DSR process, via EDM cycles and RELAX procedure.
The approach is sequential. Each trial starting set is submitted first to the tangent procedure and then to direct space procedures.
The program stops when a figure of merit is larger than a given threshold.
In Sir2019 the MDM procedure is the default choice for structures up to 300 non-hydrogen atoms in asymmetric unit.
Standard Direct Methods (SDM) procedure
Even in this case a multisolution approach is used; the phasing procedures involves, for each trial, the application of the tangent step to Nlarge reflections (those selected by the normalization process), starting from a subset of random phases. The P10 formula is applied and the most reliable negative quartets are actively used during the phasing process.
An early figure of merit (eFOM) is computed for each tangent trial: eFOM (Burla, Carrozzini et al. 2003a, Burla, Caliandro et al. 2004b) is expected to be a maximum for the most promising phase sets. Only the best trial solutions, sorted by eFOM, are submitted to the DSR procedure.
The VLD (Vive la Difference) procedure
As previously described in the section Phase extension and refinement methods, random phases are assigned to the target structure factors F. Then n EDM cycles are alternated with a DEDM (difference electron density) calculation and modification to recover new estimates of the model structure factors. The procedure is cyclic until a suitable figure of merit stops the calculations.
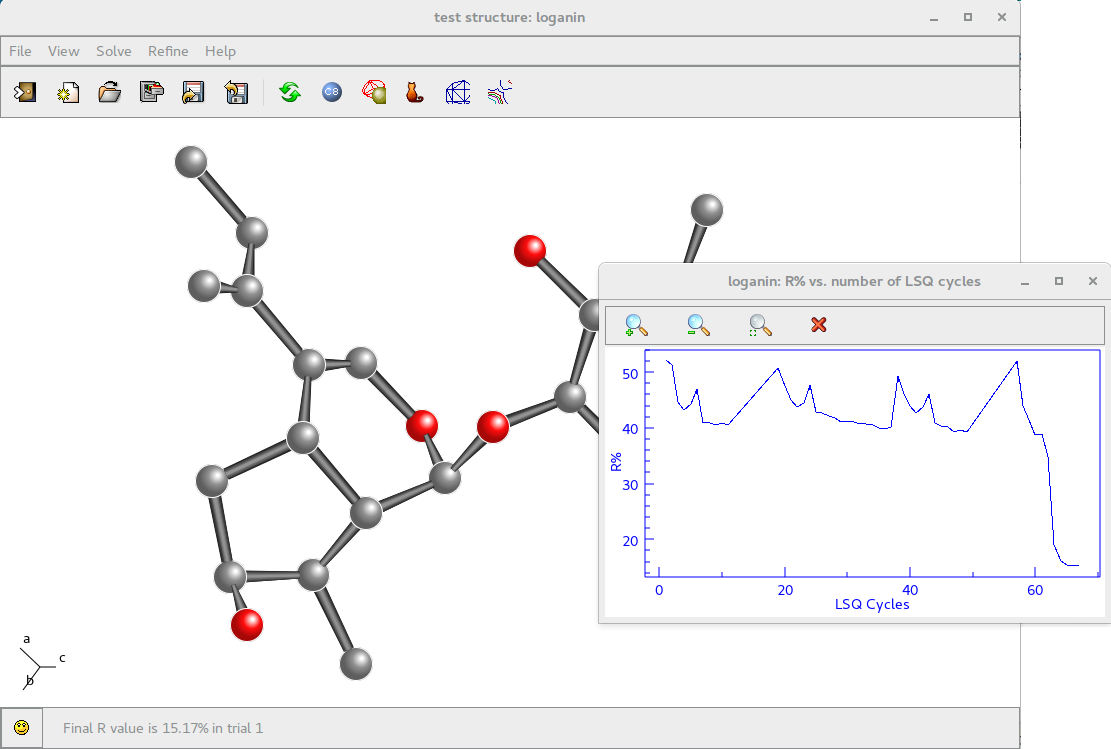
As an example the screenshot of the crystal structure solution obtained using VLD is reported. The Rf vs VLD cycle trend is shown in the small window.
Patterson deconvolution procedure
Sir2019 uses the Patterson approach (Bürger, 1959; Richardson & Jacobson, 1987; Sheldrick, 1992) mostly for the ab initio solution of large molecules and proteins.
The Patterson deconvolution techniques are based on the use of implication transformations, of the minimum superposition function (SMF) and on the superposition techniques. The procedure, described by Burla, Caliandro et al. (2004a; 2006a,b), includes filtering algorithms (to eliminate the residual Patterson symmetry, to break off non-crystallographic symmetries produced by the deconvolution process, and to restate the non-centrosymmetric nature of the electron density map), EDM, VLD and FL techniques (included in the DSR procedure) for improving and extending the phases.
Several new algorithms like C-MAP and SNIP (Caliandro et al., 2014) have been devised and implemented in Sir2019. An Automated Model Building procedure (via Buccaneer, Nautilus, ARP/wARP or Phenix) of the final electron density map is now part of the procedure.
When MR techniques are used the correct enantiomorph of the protein is automatically fixed by the model. In ab initio and SAD/MAD cases the final phases and their enantiomorph one at the time are automatically submitted to Buccaneer: alpha-helices are used to identify the correct enantiomorph.